Space-time large deviations in capacity-constrained relay networks

Abstract

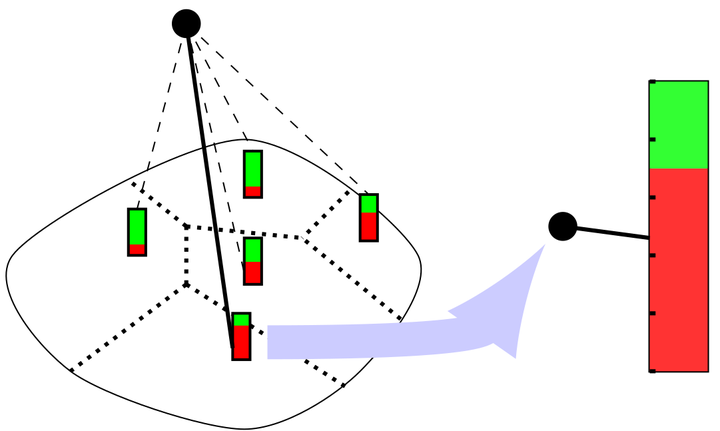
We consider a single-cell network of random transmitters and fixed relays in a bounded domain of Euclidean space. The transmitters arrive over time and select one relay according to a spatially inhomogeneous preference kernel. Oncea transmitter is connected to a relay, the connection remains and the relay is occupied. If an occupied relay is selected by another transmitters with later arrival time, this transmitter becomes frustrated. We derive a large deviation principle forthe space-time evolution of frustrated transmitters in the high-density regime.