Large deviations

What is the probability that a random geometric graph in a sampling window has atypically few or atypically many edges or triangles? What are the sources leading to such rare events? These examples illustrate the core questions of large devations in geometric probability.

For combinatorially defined random graphs, developing appropriate tools to understand the precise nature of large deviations has been the starting point for a vibrant research direction. In the geometric setting, the process-level large deviation theory for the Poisson point process could explain large deviations in a variety of examples satisfying stabilization and exponential moment conditions. However, for instance for the edge count in the random geometric graph such moment conditions do not hold and the process-level theory breaks down. In analogy to sums of heavy-tailed random variables, the large-deviation behavior is coined by a fascinating condensation phenomenon.

Another example for condensation in the setting of stochastic geometry are upper large deviations of power-weighted distances in the $k$-nearest neighbor graph. In a paper with D. Willhalm, we show that if the power is larger than the dimensions, then only a finite number of edges contribute substantially to an atypically large total power-weighted edge length.

In a paper with B. Jahnel and A. Tóbiás, we elucidate how sprinkling-based regularization makes it possible to determine lower large deviations for clique counts in the random geometric graph, intrinsic volumes of Poisson-Voronoi cells, as well as power-weighted edge lengths in the random geometric, $k$-nearest neighbor and relative neighborhood graph. In light of these developments, stochastic geometry and spatial random networks gain increasing acceptance among engineers, as they reveal novel insights into large systems subject to random effects.

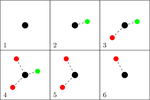
While the previous paragraphs illustrate the recent progress in the understanding of rare events in random networks, for a variety of applications it is not acceptable to encode only binary interactions in the form of edges. Here, simplicial complexes offer the alternative of modeling far more complex higher-order interactions. In a paper with T. Owada, we prove a large deviation principle for the point process associated to $k$-element connected components in the sparse regime. As concrete examples of topological invariants, we consider persistent Betti numbers of geometric complexes and the number of Morse critical points of the min-type distance function.

While the large deviation principle pertains an asymptotic regime, the insights gained through this investigation are also of value for specific bounded domains, most prominently when constructing efficient estimators for rare-event probabilities. In a paper with S.B. Moka, T. Taimre and D.P. Kroese, we develop conditional Monte Carlo algorithms for estimating rare-event probabilities for the random geometric graph. Building on conceptual insights from large-deviations theory, we illustrate that importance sampling using a Gibbsian point process can further substantially reduce the estimation variance.

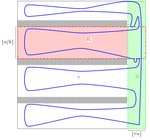
In 1934, Eugene Wigner introduced his landmark model of a gas of electrons in matter. A finite number of electrons are distributed in the Euclidean space and are subject to repulsive Coulomb forces. To confine the particles in a bounded domain, Wigner assumes the existence of a uniform background charge, approximating contributions from positive atoms. This ensures overall neutrality. The Feynman-Kac formalism makes it possible to express the quantum-mechanical statistics – i.e., Maxwell-Boltzmann, Bose-Einstein and Fermi-Dirac – in terms of expectation with respect to Brownian bridges subject to an interaction governed by a time-integration of the potential energy above.

Together with P. Jung and S. Jansen, we derive a level-3 large deviation principle for the associated Gibbsian process on an elongated strip (code).

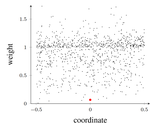
Spatial preferential attachment networks were introduced by E. Jacob and P. Mörters to illustrate how embedding a complex network in a Euclidean space can induce a positive clustering coefficient. More precisely, the nodes $X_1,X_2,\dots$ are distributed independently and uniformly on the unit torus and as a new node $X_i$ is born at time $T_i$, it connects to any older node $X_j$ independently with probability $\phi\Big(\frac{T_i|X_i-X_j|^2}{\gamma\cdot deg_{T_i-}(X_j)}\Big)$, where $\deg_{T_i-}(X_j)$ denotes the in-degree of $X_j$ at time $T_i-$. The birth times are uniformly on the interval $[0, n]$ and the parameter $\gamma>0$ controls the strength of the bias towards stronger nodes. Moreover, $\varphi:[0,\infty) \to [0,1]$ is a decreasing profile function whose integral is normalized to 1/2. For the plotting, we choose a power-law decay with exponent $\delta>1$.

In a paper with C. Mönch, we analyze shortest distances in this network and prove a large deviation principle for the neighborhood structure (code).