Abstract
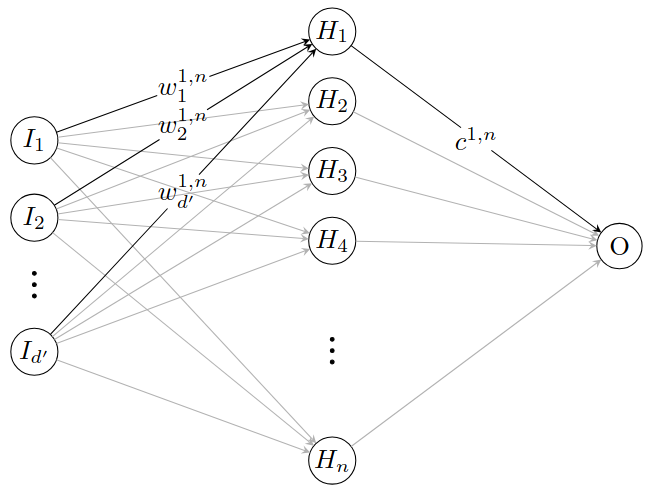
We study large deviations in the context of stochastic gradient descent for one-hidden-layer neural networks with quadratic loss. We derive a quenched large deviation principle, where we condition on an initial weight measure, and an annealed large deviation principle for the empirical weight evolution during training when letting the number of neurons and the number of training iterations simultaneously tend to infinity. The weight evolution is treated as an interacting dynamic particle system. The distinctive aspect compared to prior work on interacting particle systems lies in the discrete particle updates, simultaneously with a growing number of particles.
Type
Publication
Stoch. Dyn.