Topological data analysis

Topological data analysis (TDA) is based on an equally simple as intriguing principle: leverage invariants from algebraic topology to gain novel insights into data. While initially, TDA started as a vague idea, it is now applied by researchers working in astronomy, biology, finance and materials science. Since also data sets collected by businesses are rapidly growing in dimensionality and complexity, mastering the versatile tools from TDA is on the verge of becoming a key asset for data scientists working in industry.

However, the excitement about the spectacular novel results comes with a caveat: new insights are often presented through plots that are visually compelling, but critically lack a solid statistical underpinning. In order to decide scientifically whether any purported findings are indeed significant or merely an incarnation of chance, the rigor of statistical tests is essential.

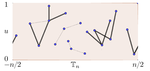
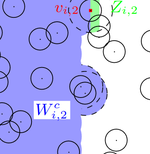
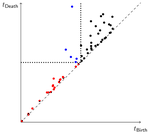
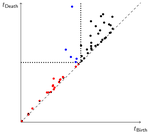
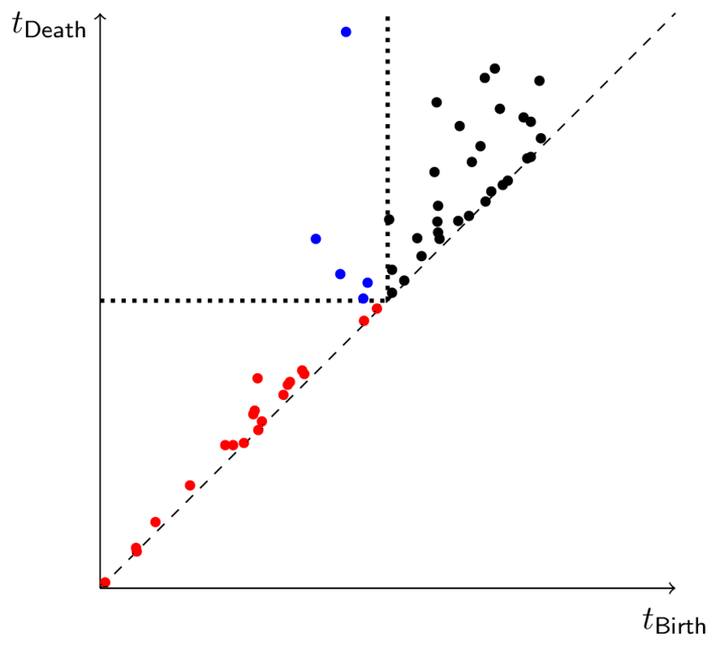
The major driving force behind the success of TDA is the persistence diagram. Loosely speaking, it is constructed on a process of growing balls centered at a cloud of data points. In this growth process, at specific time instances, topological features such as loops or higher-dimensional holes may form. When they become covered by the growing balls, such features disappear again, thus eventually leading to a family of birth- and death times collected in the persistence diagram.

Within this stream of research, in a paper/ code with C.A.N. Biscio, N. Chenavier and A.M. Svane, we develop a goodness-of-fit test for point patterns based on a functional CLT for the persistence diagram.

Furthermore, the field of TDA is not limited to point patterns, but extends to richer structures. For instance, the persistence diagram has been used to analyze complex arterial networks in the brain. In a paper/ code with J.T.N. Krebs, we are establishing a functional CLT also for spatial random networks such as the directed spanning forest. Moreover, in materials science, measuring 3D data of a material is often prohibitively expensive, whereas it is substantially more practical to gather several 2D slices. Devising statistical tests in this context is challenging since the topologies in adjacent slices are highly correlated. In a paper with A. Cipriani and M. Vittorietti, we rely on the tools of persistence in order to track such correlations over several slices.

When analyzing persistent homology, practitioners often look for features living for exceptionally long periods of time, and then draw conclusions if they do occur. However, how can we decide whether the observed long life times come from genuinely interesting phenomena and are not a mere incarnation of chance? In a paper/ code with N. Chenavier, we move one step closer to statistical applications and establish Poisson approximation results for extremal life times of loops and holes in large sampling windows.

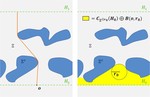
Understanding the statistical foundations of the persistence diagram is an important problem. There are, however, many situations for which it is natural to simultaneously consider multiple filtration parameters, e.g. when a point cloud comes equipped with additional measurements taken at the locations of the data. Multiparameter persistent homology was introduced to accommodate such multifiltrations, and it has become one of the most active areas of research within TDA, with exciting progress on multiple fronts. In a paper with M.B. Botnan, we offer a first step towards a rigorous statistical foundation of multiparameter persistence. Notably, we establish the strong consistency and asymptotic normality of the multiparameter persistent Betti numbers in growing domains.