Abstract
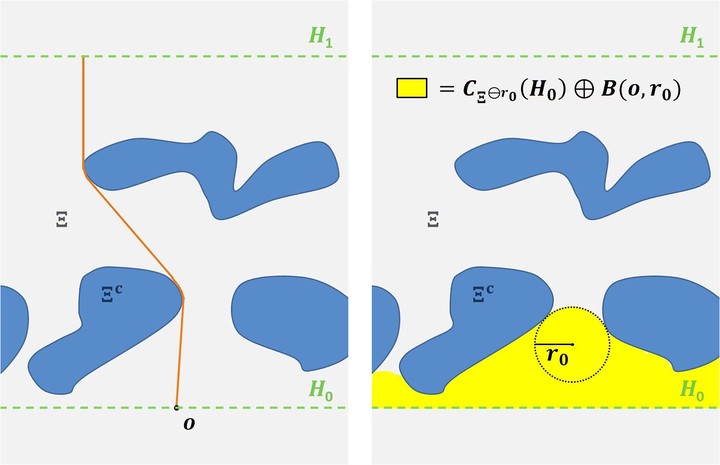
We investigate the problem of estimating geodesic tortuosity and constrictivity as two structural characteristics of stationary random closed sets. They are of central importance for the analysis of effective transport properties in porous or composite materials. Loosely speaking, geodesic tortuosity measures the windedness of paths, whereas the notion of constrictivity captures the appearance of bottlenecks resulting from narrow passages within a given materials phase. We first provide mathematically precise definitions of these quantities and introduce appropriate estimators. Then, we show strong consistency of these estimators for unboundedly growing sampling windows. In order to apply our estimators to real data sets, the extent of edge effects needs to be controlled. This is illustrated using a model for a multiphase material that is incorporated in solid oxide fuel cells.