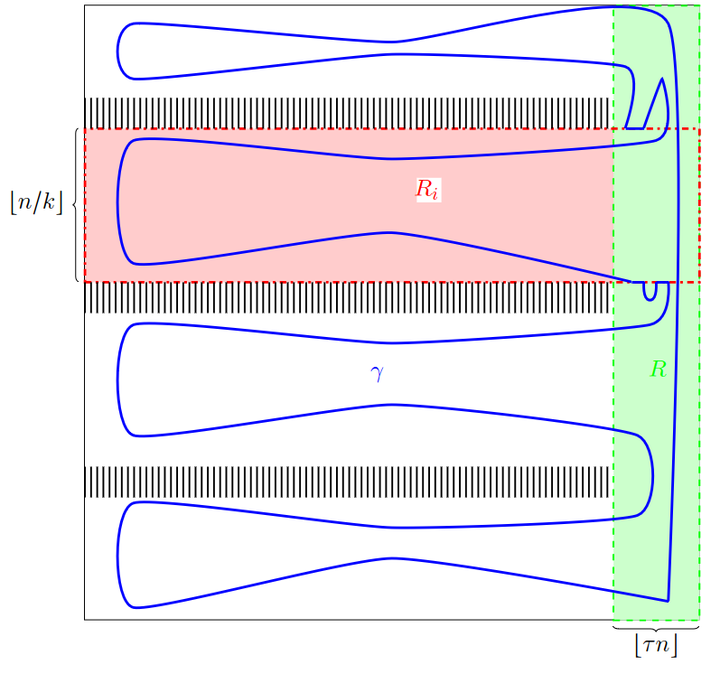
Abstract
Isoperimetric profile describes the minimal boundary size of a set with a prescribed volume. Itai Benjamini conjectured that the isoperimetric profile of the giant component in supercritical percolation experiences an averaging effect and satisfies the law of large numbers. This conjecture was settled by Biskup-Louidor-Procaccia-Rosenthal for 2D percolation, and later resolved by Gold for higher-dimensional lattices. However, more refined properties of the isoperimetric profile, such as fluctuations and large deviations, remain unknown. In this paper, we determine the large deviation probabilities of the isoperimetric constant in 2D supercritical percolation, answering the question by Biskup-Louidor-Procaccia-Rosenthal. Interestingly, while the large deviation probability is of surface order in the entire upper tail regime, a phase transition occurs in the lower tail regime, exhibiting both surface and volume order large deviations.