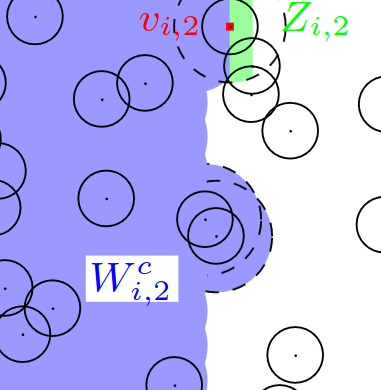
Abstract
This work improves the existing central limit theorems (CLTs) on Gibbs processes in three aspects. First, we derive a CLT for weakly stabilizing functionals, thereby improving on the previously used assumption of exponential stabilization. Second, we show that this CLT holds for interaction ranges up to the percolation threshold of the dominating Poisson process. This avoids imprecise branching bounds from graphical construction. Third, by extending the concept of Stein couplings from the Poisson to the Gibbs setting, we provide a quantitative CLT in terms of Kolmogorov bounds for normal approximation. An important conceptual ingredient in these advances are extensions of disagreement coupling adapted to increasing windows and to the comparison at multiple spatial locations.