Large deviations of one-hidden-layer neural networks

Abstract

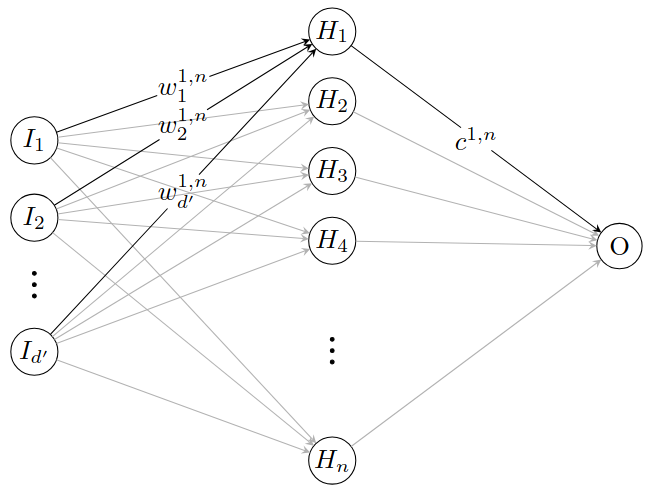
In this work, we study large deviation properties of the covariance process in fully connected Gaussian deep neural networks. More precisely, we establish a large deviation principle (LDP) for the covariance process in a functional framework, viewing it as a process in the space of continuous functions. As key applications of our main results, we obtain posterior LDPs under Gaussian likelihood in both the infinite-width and mean-field regimes. The proof is based on an LDP for the covariance process as a Markov process valued in the space of non-negative, symmetric trace-class operators equipped with the trace norm.