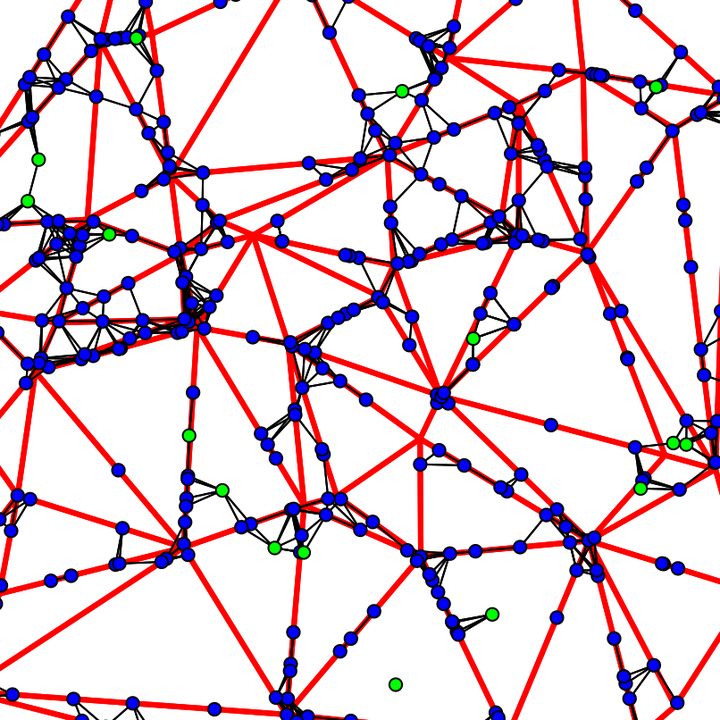
Higher-order networks

With the massively growing sources of data in the very recent years, we are now realizing that for the vast majority of networks, viewing them as a collection of entities linked by binary relations means a gross simplification. To describe the phenomenon of learning in the human brain, we need to understand the joint neural activity of groups of three or more neurons, most of today’s scientific papers have three or more authors, the assumption of chemical bonds between molecules is only a simplification of the actual quantum mechanics, etc. Traditionally, network science has analyzed networks as graphs consisting of nodes and binary relations between them. However, when higher-order relations are present, binary networks provide an incomplete picture. Complex networks with higher-order relations can instead be represented by a simplicial complex, where the graph formed by nodes with binary relations is amended by triangles, tetrahedrons, and higher-dimensional simplices corresponding to third, fourth or higher-order relations, respectively. These examples illustrate the urgent need to move beyond the simple binary relations considered in classical network science and capture the effects of higher-order interactions. In a recent work with P. Juhász, we investigated the asymptotic behavior of large spatial models for higher-order networks and illustrated the use on datasets from the arxiv collaboration networks. In a follow-up work with P. Juhász and B. Jahnel we extended the analysis to dynamic networks.

Models for stochastic learning

Spatial random networks are also of central importance in neuroscience. Indeed, neurons fire randomly and the weight of one of the incident synapses is incremented. The selection of the synapse is proportional to its weight to a power $\alpha >0$. Depending on whether $\alpha$ is larger, equal or smaller than 1, the process is in the superlinear, linear or sublinear regime. In a paper/ follow-up with M. Holmes and V. Kleptsyn, we study the model on countable graphs and investigate whether it is possible to arrive at a percolating but sparse network of relevant edges.

D2D networks

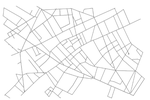
Traditionally, wireless networks were based on the assumption of a relatively small number of users in a fixed system of base stations. The simple network structure allows to simulate the entire system with all network participants to a high degree of detail thereby creating the foundations for deeper case studies. However, rapidly advancing technological developments are increasingly calling the feasibility of this approach into question:

1. Explosion of network size. The Internet of Things (IoT) leads to an enormous increase in the network components. Even with powerful computing facilities, systems consisting of several thousand nodes are difficult to reproduce in detail.
2. Complex network topologies. While previous networks were predominantly hierarchical, now heterogeneous and self-organizing structures are becoming increasingly prevalent. This substantially increases the possible interactions between network participants.
3. Limited reliability. The surge in number and degree of interconnectedness of the indi- vidual components also reduces reliability. The failure of individual components is no longer exceptional, but rather becomes a core characteristic of modern networks.

In light of these developments, percolation theory, stochastic geometry and spatial random networks gain increasing acceptance among engineers, as they reveal novel insights into large systems subject to random effects.

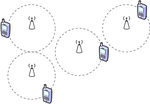
In the context of the Internet of Things and in 5G cellular networks, Device-to-Device (D2D) communication plays a key role. This technology aims to reduce the load on the base station by allowing users to communicate with one another - either directly or through several intermediate steps. Even though D2D communication holds the promise of increasing the throughput in future network architectures substantially, it marks a paradigm change from the classical hierarchical structures: D2D networks are highly heterogeneous and connections between individual network participants unreliable. Hence, network operators face the following questions

1. What proportion of users can rely on D2D communication to other users?
2. What proportion of users can connect to a base station in a bounded number of hops?

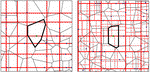
The mathematical treatment of these questions falls into the domain of continuum percolation. The particular traits in wireless networks have inspired novel percolation models that are both rooted in applications, and bring also new mathematical facets. Prototypical examples are bounded-hop percolation and Cox percolation. One of the major findings of percolation theory is the occurrence of a phase transition. That is, there is a uniquely defined critical threshold for the device density such that below this threshold data exchange is only possible in a small neighborhood of the considered device. On the other hand, above this threshold, a giant connected component emerges that allows a positive proportion of all devices to exchange data via D2D transmissions. A key result in classical continuum percolation is that this phase transition is sharp. That is, in the subcritical regime, the probability of observing long-range connections not only tends to 0 but does so at an exponential speed. In a paper with B. Jahnel and S. Muirhead, we extend this result to Cox percolation.

In a paper with G. Last, we address the question of making sense of the densest possible thinning of a stationary particle process. By assigning the value 1 to particles within the thinning and the value 0 to particles outside the thinning, we can think of this problem as finding an optimal binary marking. The challenge of optimal markings also arises in an entirely different application context, namely wireless networks. Here, an infinite system of transmitters can send messages to dedicated nearby receivers. However, since simultaneous transmissions of all network participants would cause massive interference, the transmitters should access the network only with a certain probability. If we aim at maximizing a global throughput-oriented characteristic such as proportional fairness, then we can think of this task as finding a $[0,1]$-marking of the transmitters with optimal access probabilities.

Together with B. Blaszczyszyn, we study existence and equivalence of intensity-optimal markings and locally optimal markings as two possible formalizations of the concept of optimal markings for infinite-volume particle configurations.

All of the aforementioned results concern static networks. However, a core characteristic of modern D2D networks is that they are dynamic. That is, the nodes do not remain at a single location on the street system but can follow a complex mobility pattern. In a paper/ follow-up together with B. Jahnel and E. Cali, we We study the effects of mobility on two crucial characteristics in multi-scale dynamic networks: percolation and connection times. Our analysis provides insights into the question, to what extent long-time averages are well-approximated by the expected values of the corresponding quantities, i.e., the percolation and connection probabilities. In particular, we show that in multi-scale models, strong random effects may persist in the limit.