A Spatial Small-World Graph Arising from Activity-Based Reinforcement

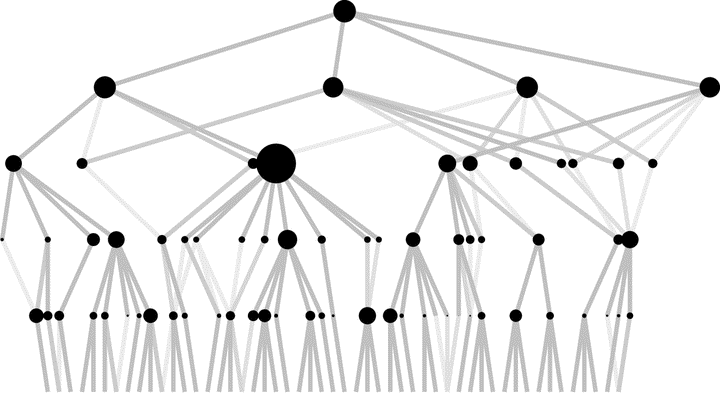
Abstract

In the classical preferential attachment model, links form instantly to newly arriving nodes and do not change over time. We propose a hierarchical random graph model in a spatial setting, where such a time-variability arises from an activity-based reinforcement mechanism. We show that the reinforcement mechanism converges, and prove rigorously that the resulting random graph exhibits the small-world property. A further motivation for this random graph stems from modeling synaptic plasticity.