WARM percolation on a regular tree in the strong reinforcement regime

Abstract

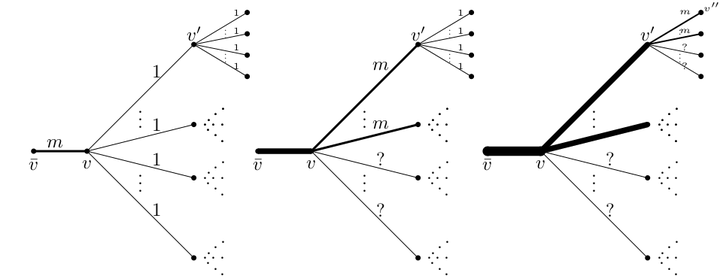
We consider a class of reinforcement processes, called WARMs, on tree graphs. These processes involve a parameter $\alpha$ which governs the strength of the reinforcement, and a collection of Poisson processes indexed by the vertices of the graph. It has recently been proved that for any fixed bounded degree graph with Poisson firing rates that are uniformly bounded above, in the very strong reinforcement regime ($\alpha \gg 1$ sufficiently large depending on the maximal degree), the set of edges that “survive” (i.e. that are reinforced infinitely often by the process) has only finite connected components. The present paper is devoted to the construction of example in the opposite direction, that is, with the set of surviving edges having infinite connected components. Namely, we show that for each fixed $\alpha > 1$ one can find a regular rooted tree and firing rates that are uniformly bounded from above, for which there are infinite components almost surely. Joining such examples, we find a graph (with unbounded degrees) on which for any $\alpha > 1$ almost surely there are infinite connected components of surviving edges.