Abstract
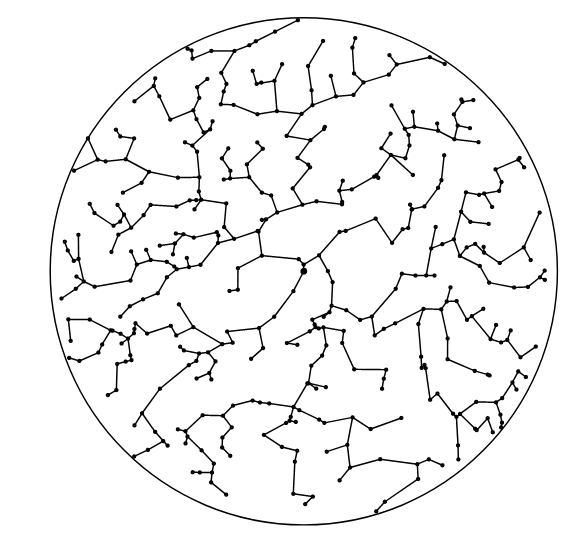
We consider transport networks with nodes scattered at random in a large domain. At certain local rates, the nodes generate traffic flows according to some navigation scheme in a given direction. In the thermodynamic limit of a growing domain, we present an asymptotic formula expressing the local traffic flow density at any given location in the domain in terms of three fundamental characteristics of the underlying network: the spatial intensity of the nodes together with their traffic generation rates, and of the links induced by the navigation. This formula holds for a general class of navigations satisfying a link-density and a sub-ballisticity condition. As a specific example, we verify these conditions for navigations arising from a directed spanning tree on a Poisson point process with inhomogeneous intensity function.