Connectivity of random geometric graphs related to minimal spanning forests

Abstract

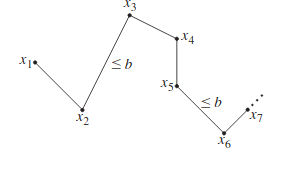
The a.s. connectivity of the Euclidean minimal spanning forest $\text{MSF}(X)$ on a homogeneous Poisson point process $X\subset {\mathbb{R}}^d$ is an open problem for dimension $d>2$. We introduce a descending family of graphs $(G_n{)}_n$ that can be seen as approximations to the $\text{MSF}$ in the sense that $\text{MSF}(X)=\bigcap _n{G}_n(X)$. For $n=2$ one recovers the relative neighborhood graph or, in other words the $\beta$-skeleton, with $\beta =2$. We show that a.s. connectivity of $G_n(X)$ holds for all $n\ge 2$, for all dimensions $d\ge 2$, and also for point processes $X$ more general than the homogeneous Poisson point process. More precisely, a.s. connectivity holds if certain continuum percolation thresholds are strictly positive or, more generally, if a.s. $X$ does not admit generalized descending chains.