Percolation for D2D networks on street systems
Abstract
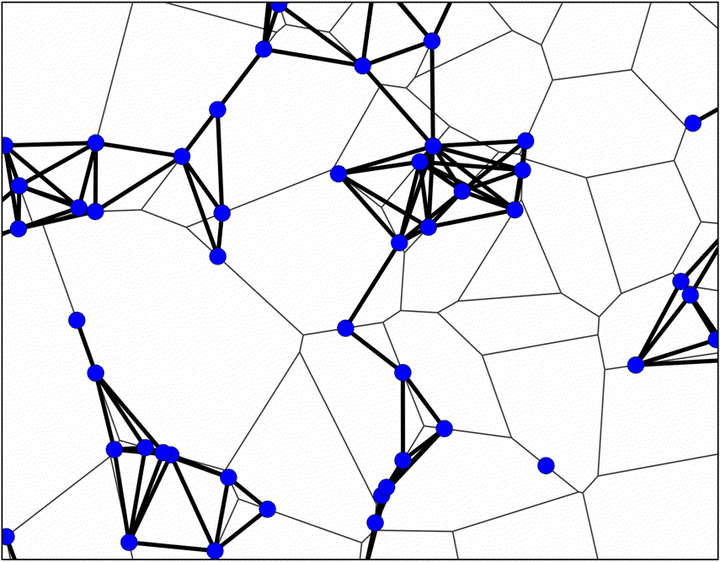
We study fundamental characteristics for the connectivity of multi-hop D2D networks. Devices are randomly distributed on street systems and are able to communicate with each other whenever their separation is smaller than some connectivity threshold. We model the street systems as Poisson-Voronoi or Poisson-Delaunay tessellations with varying street lengths. We interpret the existence of adequate D2D connectivity as percolation of the underlying random graph. We derive and compare approximations for the critical device-intensity for percolation, the percolation probability and the graph distance. Our results show that for urban areas, the Poisson Boolean Model gives a very good approximation, while for rural areas, the percolation probability stays far from 1 even far above the percolation threshold.