Abstract
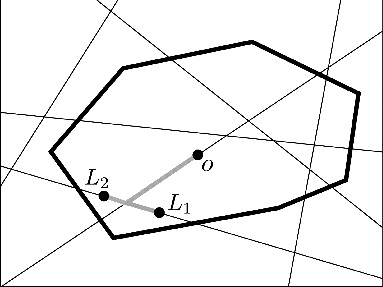
We provide a parametric modeling approach suitable for various kinds of hierarchical networks based on random geometric graphs. In these networks, we have two kinds of components, so-called high-level components (HLC) and low-level components (LLC). Each HLC is associated with a serving zone and all LLC within this area are connected to the corresponding HLC. So-called sparse LLC networks, where only a few LLC occur in the typical serving zone, are a non-negligible subdomain when investigating hierarchical networks. Therefore, we supply distributional results for structural characteristics where two LLC are independently and uniformly distributed along the segment system of the typical serving zone. In particular, we are interested in the joint distribution of three quantities, namely the length of the joint part of the shortest paths from the LLC to the HLC as well as the lengths of the corresponding disjoint remaining parts. In order to provide a parametric, three-dimensional distribution function for these random variables, we utilize a pseudo-maximum likelihood approach. More precisely, we fit parametric approximation formulas to the marginal density functions as well as parametric copula functions that match with the observed correlation structure. We also provide an asymptotic result for the joint distribution of the connection lengths as the size of the typical cell increases unboundedly. This general modeling approach is explicitly explained for the case that the random geometric graph is formed by the edges of random tessellations.