Higher-order spatial networks

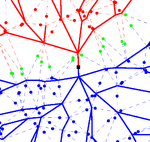
With the rapid growth of data sources in recent years, it has become increasingly clear that modeling networks purely in terms of binary relations often constitutes a severe oversimplification. In many applications, interactions naturally involve groups of three or more entities, motivating the study of higher-order networks. Such systems can be represented by simplicial complexes, where nodes, edges, triangles, tetrahedra, and higher-dimensional simplices encode multi-way interactions.

In a paper with P. Juhász, we study large spatial models for higher-order networks and investigate their asymptotic behavior, with applications to collaboration networks such as the arXiv coauthorship graph. In a follow-up work with P. Juhász and B. Jahnel, we extend the analysis to dynamic higher-order networks, capturing temporal evolution of multi-way interactions.

Models for stochastic learning and reinforcement

Spatial random networks also arise naturally in models of learning and reinforcement, particularly in neuroscience. In these models, neurons fire randomly and synaptic weights are updated proportionally to their current strength, leading to reinforcement dynamics governed by a parameter $\alpha >0$. Depending on whether $\alpha$ is smaller than, equal to, or larger than one, the system exhibits qualitatively different regimes.

In a paper/ follow-up with M. Holmes and V. Kleptsyn, we study such reinforced processes on countable graphs and investigate whether it is possible to obtain networks that are sparse yet percolating in the strong reinforcement regime.

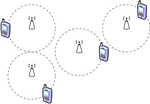
Device-to-device and spatial wireless networks

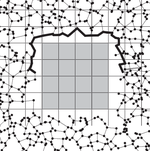
In modern wireless systems, such as the Internet of Things and 5G networks, device-to-device (D2D) communication plays a central role. These networks are inherently heterogeneous, unreliable, and large-scale, rendering detailed simulation infeasible and motivating probabilistic modeling approaches.

The mathematical analysis of D2D networks naturally leads to models from stochastic geometry and continuum percolation. Prototypical examples include bounded-hop percolation and Cox percolation, which capture spatial inhomogeneities and multi-scale effects. One of the central results in classical continuum percolation is the sharpness of the phase transition between disconnected and connected regimes.

In a paper with B. Jahnel and S. Muirhead, we establish sharp phase transitions for Cox percolation, extending classical results to spatially inhomogeneous settings.

Optimal markings and interference management

In large wireless networks, interference constraints require transmitters to access the medium only with certain probabilities. This leads naturally to optimization problems over marked point processes. In a paper with G. Last, we study maximal hard-core thinnings and optimal binary markings of stationary particle processes.

Together with B. Błaszczyszyn, we further investigate existence and equivalence of intensity-optimal and locally optimal markings, providing a rigorous foundation for throughput-oriented optimization in infinite wireless networks.

Dynamic spatial networks

A defining characteristic of modern spatial networks is their dynamic nature, as nodes may move or connections may evolve over time. In a paper/ follow-up with B. Jahnel and E. Cali, we study multi-scale dynamic networks and analyze the impact of mobility on percolation and connection times. We show that strong random effects may persist in the long-time limit, highlighting fundamental differences between static and dynamic spatial models.

Fluctuations and limit theorems for random connection models

Beyond connectivity and percolation, an important aspect of spatial network models is the quantitative description of fluctuations of network observables. In a series of recent works, we study limit theorems for random connection models with spatial, temporal, and structural heterogeneity. In a paper with M. Brun, P. Juhász and M. Otto, we introduce random connection hypergraphs and analyze higher-order interactions beyond pairwise connections. In a paper with N. Heerten and M. Otto, we develop a cumulant-based approach to normal and Poisson approximation for weighted random connection models. Further results include normal approximations for subgraph counts in age-dependent random connection models, functional limit theorems for edge counts in dynamic random connection hypergraphs, and limit theorems in heavy-tailed regimes, providing a unified probabilistic description of fluctuations in large spatial networks.